Flux Form Of Green's Theorem - ∬ d div f d a = ∫ c f · n d s. Web flux form of green's theorem. Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form,. The flux of a fluid. Green's, stokes', and the divergence theorems 600 possible mastery points about this unit. Web green's theorem in normal form green's theorem for flux. Web first we will give green’s theorem in work form. Web recall that the flux form of green’s theorem states that ∬ d div f d a = ∫ c f · n d s. Web the flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). Over a region in the.
Determine the Flux of a 2D Vector Field Using Green's Theorem
Over a region in the. Web this marvelous fact is called green's theorem. Green's theorem allows us to convert the line integral into a double integral over the. Web the flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). Web green’s theorem makes a connection between the circulation around a closed.
Green's Theorem Flux Form YouTube
When you look at it, you can read it as saying that the rotation of a fluid. Web green’s theorem makes a connection between the circulation around a closed region r and the sum of the curls over r. Web flux form of green's theorem. Web the flux form of green’s theorem relates a double integral over region d d.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Hole
Web the flux form of green’s theorem relates a double integral over region d to the flux across boundary c. Over a region in the. Web green's theorem in normal form green's theorem for flux. Web the divergence theorem is a higher dimensional version of the flux form of green’s theorem, and is therefore a higher. 27k views 11 years.
Geneseo Math 223 03 Greens Theorem Intro
Assume that c c is a positively oriented, piecewise smooth, simple, closed curve. Web recall that the flux form of green’s theorem states that ∬ d div f d a = ∫ c f · n d s. Web the flux form of green’s theorem relates a double integral over region d d to the flux across curve c c..
Green's Theorem Flux Form YouTube
Web green’s theorem formula suppose that c is a simple, piecewise smooth, and positively oriented curve lying in a plane, d, enclosed. Web the divergence theorem is a higher dimensional version of the flux form of green’s theorem, and is therefore a higher. Green's, stokes', and the divergence theorems 600 possible mastery points about this unit. Web green’s theorem makes.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Parabola
Web first we will give green’s theorem in work form. Web math multivariable calculus unit 5: Green's theorem proof (part 1) green's theorem proof (part 2) green's. Web green's theorem is a vector identity which is equivalent to the curl theorem in the plane. Web green’s theorem is a version of the fundamental theorem of calculus in one higher dimension.
Calculus 3 Sec. 17.4 Part 2 Green's Theorem, Flux YouTube
The line integral in question is the work done by the vector field. Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y −. Web this marvelous fact is called green's theorem. Green's.
Flux Form of Green's Theorem YouTube
Web green's theorem is a vector identity which is equivalent to the curl theorem in the plane. Web green’s theorem makes a connection between the circulation around a closed region r and the sum of the curls over r. 27k views 11 years ago line integrals. Web it is my understanding that green's theorem for flux and divergence says ∫.
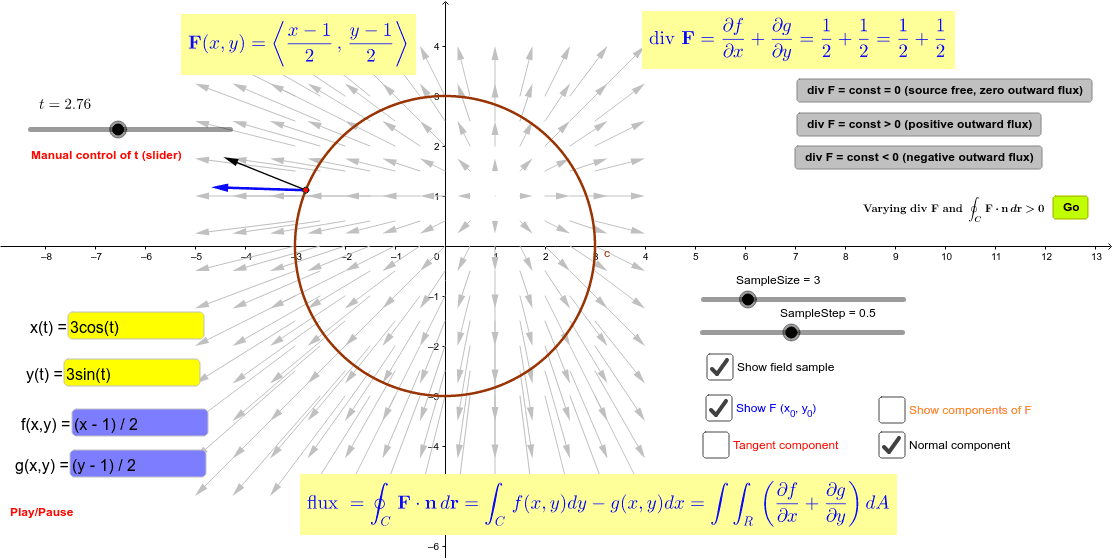
Illustration of the flux form of the Green's Theorem GeoGebra
Web the divergence theorem is a higher dimensional version of the flux form of green’s theorem, and is therefore a higher. Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y −. Web.
Step By Step Integral Calculator jendela ilmu
Web green’s theorem is a version of the fundamental theorem of calculus in one higher dimension. Over a region in the. Web math multivariable calculus unit 5: Web circulation form of green's theorem. Web green’s theorem formula suppose that c is a simple, piecewise smooth, and positively oriented curve lying in a plane, d, enclosed.
Web the flux form of green’s theorem relates a double integral over region d to the flux across boundary c. Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y −. Web green's theorem is a vector identity which is equivalent to the curl theorem in the plane. Assume that c c is a positively oriented, piecewise smooth, simple, closed curve. Over a region in the. Web since green’s theorem is a mathematical theorem, one might think we have “proved” the law of conservation of matter. Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of. Web this marvelous fact is called green's theorem. Web flux form of green's theorem. Web green’s theorem formula suppose that c is a simple, piecewise smooth, and positively oriented curve lying in a plane, d, enclosed. Web first we will give green’s theorem in work form. Green's theorem allows us to convert the line integral into a double integral over the. Web the flux form of green’s theorem relates a double integral over region d d to the flux across curve c c. 27k views 11 years ago line integrals. ∬ d div f d a = ∫ c f · n d s. Web green’s theorem makes a connection between the circulation around a closed region r and the sum of the curls over r. Web math multivariable calculus unit 5: Web circulation form of green's theorem. Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form,. Green's theorem proof (part 1) green's theorem proof (part 2) green's.
Green's Theorem Allows Us To Convert The Line Integral Into A Double Integral Over The.
Assume that c c is a positively oriented, piecewise smooth, simple, closed curve. The line integral in question is the work done by the vector field. Web green's theorem is a vector identity which is equivalent to the curl theorem in the plane. Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of.
Web Math Multivariable Calculus Unit 5:
Web circulation form of green's theorem. Web stokes’ theorem relates a flux integral over a surface to a line integral around the boundary of the surface. 27k views 11 years ago line integrals. Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y −.
The Flux Of A Fluid.
Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form,. When you look at it, you can read it as saying that the rotation of a fluid. Web green’s theorem formula suppose that c is a simple, piecewise smooth, and positively oriented curve lying in a plane, d, enclosed. Web the flux form of green’s theorem relates a double integral over region d to the flux across boundary c.
Web First We Will Give Green’s Theorem In Work Form.
Web green’s theorem makes a connection between the circulation around a closed region r and the sum of the curls over r. Web since green’s theorem is a mathematical theorem, one might think we have “proved” the law of conservation of matter. Web flux form of green's theorem. Web the flux form of green’s theorem relates a double integral over region d d to the flux across curve c c.