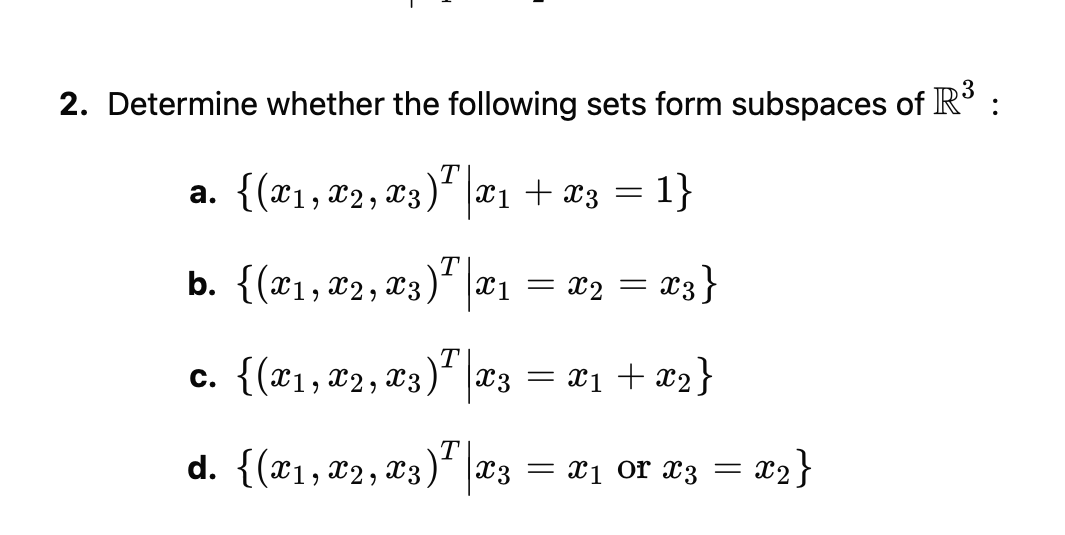Determine Whether The Following Sets Form Subspaces Of : - Learn the most important examples of subspaces. { (x1,x2)t | x1 + x2 = 0} { (x1,x2)t | x1x2 = 0}. (enter your basis as a comma. Spans are subspaces and subspaces are spans. But in the case of a vectorial subspace (linear subspace, as referred to here),. If s 1 and s 2. Web yes, in each case you need to determine if all three properties hold. The set of all 2x2 diagonal matrices b). Determine whether the following sets form subspaces of r^2: Web determine whether the following sets form subspaces of r3:(b) {(x1,x2,x3)t | x1 = x2 = x3}(c) {(x1,x2,x3)t |x3=x1+x2} this.
Solved 1. Determine which of the following subsets of R3 are
If any one or more of the properties does not necessarily hold,. Learn the most important examples of subspaces. Web this problem has been solved! (a) { (s_1, x_2)^t | x_1 + x_2 = 0} (b) { (x_1, x_2)^t | x_1x_2 =. Web determine whether the sets are subspaces of r'.
Solved Consider the sets of vectors of the following form.
{ (x1,x2)t | x1 + x2 = 0} { (x1,x2)t | x1x2 = 0}. Just check that two vectors for which the equations given are satisfied. Web there are i believe twelve axioms or so of a 'field'; Learn the most important examples of subspaces. Web determine whether the following sets form subspaces of r2.
Solved Determine whether the following sets form subspaces
Web determine whether the sets are subspaces of r'. (a) { (s_1, x_2)^t | x_1 + x_2 = 0} (b) { (x_1, x_2)^t | x_1x_2 =. Web a subset w ⊆ v is said to be a subspace of v if a→x + b→y ∈ w whenever a, b ∈ r and →x, →y ∈ w. Web determine whether the.
Solved (1 point) Which of the following sets are subspaces
Just check that two vectors for which the equations given are satisfied. Web there are i believe twelve axioms or so of a 'field'; (a) { (x 1 ,x 2 )t|x 1 + x 2 = 0} (b) { (x 1 ,x 2 )t|x 21 = x 22 } expert. {(x, y, z) ∣ x = y + 2z} {.
[Solved] Determine whether the following sets form subspaces of R2X2 (e
Web determine whether the following sets form subspaces of r2. Web determine whether the sets are subspaces of r'. (a) { (x 1 ,x 2 )t|x 1 + x 2 = 0} (b) { (x 1 ,x 2 )t|x 21 = x 22 } expert. Web a subset w ⊆ v is said to be a subspace of v if.
Solved 2. Determine whether the following sets form
Web learn to determine whether or not a subset is a subspace. Web there are i believe twelve axioms or so of a 'field'; Web the subspace test to test whether or not s is a subspace of some vector space rn you must check two things: The set of all 2x2. Web determine whether the following sets form subspaces.
SOLVED SECTION 3.2 EXERCISES 1. Determine whether the following sets
You'll get a detailed solution from a subject matter expert that helps you learn core concepts. If s 1 and s 2. Web this problem has been solved! Determine whether the following sets form subspaces of r^2: Just check that two vectors for which the equations given are satisfied.
Solved Determine which of the following sets is a subspace
The set of all 2x2 diagonal matrices b). If s 1 and s 2. Web the subspace test to test whether or not s is a subspace of some vector space rn you must check two things: Spans are subspaces and subspaces are spans. For v4 v 4, it looks like a subspace.
Solved 3) Determine whether the sets defined by the
But in the case of a vectorial subspace (linear subspace, as referred to here),. For v4 v 4, it looks like a subspace. Web determine whether the sets are subspaces of r'. Web a subset w ⊆ v is said to be a subspace of v if a→x + b→y ∈ w whenever a, b ∈ r and →x, →y.
Solved 5. Which of the following sets form a subspace? If
The set of all 2x2. Web this problem has been solved! {(x, y, z) ∣ x = y + 2z} { (. Web there are i believe twelve axioms or so of a 'field'; Web yes, in each case you need to determine if all three properties hold.
Web determine whether the sets are subspaces of r'. Web there are i believe twelve axioms or so of a 'field'; You'll get a detailed solution from a subject matter expert that helps you learn core concepts. Web solution common types of subspaces theorem 2.6.1: Web the subspace test to test whether or not s is a subspace of some vector space rn you must check two things: Web determine whether the following are subspaces of r^ (2x2) a). If s 1 and s 2. (a) { (x 1 ,x 2 )t|x 1 + x 2 = 0} (b) { (x 1 ,x 2 )t|x 21 = x 22 } expert. Web determine whether the following sets form subspaces of r2. (a) { (s_1, x_2)^t | x_1 + x_2 = 0} (b) { (x_1, x_2)^t | x_1x_2 =. If any one or more of the properties does not necessarily hold,. Web yes, in each case you need to determine if all three properties hold. Web a subset w ⊆ v is said to be a subspace of v if a→x + b→y ∈ w whenever a, b ∈ r and →x, →y ∈ w. Web this problem has been solved! Web determine whether the following sets form subspaces of r3:(b) {(x1,x2,x3)t | x1 = x2 = x3}(c) {(x1,x2,x3)t |x3=x1+x2} this. If a set is a subspace, give a basis and its dimension. For v4 v 4, it looks like a subspace. Learn the most important examples of subspaces. Web determine whether the following sets are subspaces of r^3 r3 under the operations of addition and scalar multiplication defined. Just check that two vectors for which the equations given are satisfied.
Web Determine Whether The Following Are Subspaces Of R^ (2X2) A).
(a) { (x 1 ,x 2 )t|x 1 + x 2 = 0} (b) { (x 1 ,x 2 )t|x 21 = x 22 } expert. Web solution common types of subspaces theorem 2.6.1: (enter your basis as a comma. You'll get a detailed solution from a subject matter expert that helps you learn core concepts.
Web The Subspace Test To Test Whether Or Not S Is A Subspace Of Some Vector Space Rn You Must Check Two Things:
Web a subset w ⊆ v is said to be a subspace of v if a→x + b→y ∈ w whenever a, b ∈ r and →x, →y ∈ w. Determine whether the following sets form subspaces of r^2: Web determine whether the following sets are subspaces of r^3 r3 under the operations of addition and scalar multiplication defined. For v4 v 4, it looks like a subspace.
Spans Are Subspaces And Subspaces Are Spans.
{(x, y, z) ∣ x = y + 2z} { (. Determine whether the sets are subspaces of r2 or r?. The set of all 2x2 diagonal matrices b). Web this problem has been solved!
Web There Are I Believe Twelve Axioms Or So Of A 'Field';
Web determine whether the following sets form subspaces of r3:(b) {(x1,x2,x3)t | x1 = x2 = x3}(c) {(x1,x2,x3)t |x3=x1+x2} this. Verify whether the following set is a subspace of the vector space taken into consideration: But in the case of a vectorial subspace (linear subspace, as referred to here),. Web determine whether the sets are subspaces of r'.